同学们好,我是《俄罗斯教育》有限公司(或者小狮座俄罗斯留学)的李泽龙(李经理),这篇文章是我自己在2014年9月至2019年6月期间就读乌拉尔联邦大学学习《理论数学》专业本科的一个大纲总结,在这篇文章中我会简单介绍一下数学专业本科学习的内容。 大家可以通过这篇文章详细了解俄罗斯大学数学系本科的留学压力,好了废话不多说我们直接进入文章!

一、数学系课程安排
以下我们分别按照学期介绍每一学期的课程内容
大一课程
数学分析(理论)两个学期
数学分析(习题)两个学期
高等代数(理论)两个学期
高等代数(习题)两个学期
解析几何(理论)一学期
解析几何(习题)一学期
计算机算法概论理论两学期、上机操作两学期
选修外语(法语,德语,英语,外国学生可以选俄语)两个学期
俄语理论一学期
俄国历史 理论一学期、讨论班一学期
大一还需要额外选修两门选修课,可以选择《JavaScript》、《网络构架》、《集合论》、《半群理论》、《数学分析中的数值方法》、《数理逻辑》、《初等拓补学》等。
大二课程
数学分析(理论)两学期
数学分析(实践)两学期
抽象代数和离散数学理论一学期,讨论班一学期
微分方程(理论)两学期
微分方程(实践)两学期
实变函数理论一学期,讨论班一学期
微分几何理论一学期,讨论班一学期
物理(理论)一学期
物理(实践)一学期
计算机理论两学期,实践两学期
哲学理论一学期、讨论班一学期
数据结构和SQL 一学期理论、一学期讨论版
体育一学期、社会学一学期、历史一学期
大二需要选修4门课,可选有《逼近函数》、《算法的复杂度分析》、《图论》、《线性优化》、《经济学中的数学方法》、《数学哲学》、《函数式编程中的代数方法》、《ASP.NET框架》、《微分方程的数值方法》、《傅里叶函数空间》等。
大三课程
复变函数理论一学期、实践一学期
数值分析(理论)两学期
数值分析(实践)两学期
物理(理论)一学期
泛函分析(理论)两学期
泛函分析(实践)两学期
随机过程 一学期理论、一学期实践
偏微分方程和数学物理方法 大三下学期一学期,大四上学期各一学期理论 + 实践
概率论和统计学原理(理论)一学期、实践一学期
数据库结构(SQL语言) 理论和实践一学期
面向对象的编程方法理论和实践各两学期
理论力学 两学期理论、两学期实践
数学物理方法(偏微分方程) 两学期理论、两学期实践
另外还有体育两学期、经济学一学期、管理学中的数学方法一学期、社会学一学期、心理学一学期、生命与安全一学期
外大三还需要选修6门选修课程,其中包括《调和分析》、《最优化理论》、《微分几何和流形》、《有限群理论》、《纠错码和密码学》、《Matlab编程》、《PHP前端和优化》、《拟阵》、《图论中的算法》、《代数几何》、《微分游戏理论(теория дифференциальных игр)》、《微分动力系统》、《金融随机分析》、《算子代数》、《群的表示理论》等
大四课程
数论 一学期理论
现代数学领域中的难题 讨论班两学期,其中包括
射影几何 一学期理论、一学期实践
金融数学 一学期实践
一个学生自选模块:我的是《代数学》模块,模块中包括:
调和函数 一学期实践课程
函数的优化理论 一学期实践课程
以及两门任意选修课、毕业论文、国考和本科毕业答辩,然后就毕业了。

二、数学系本科深度如何?
由于我自己非常喜欢代数学理论,所以我的本科主要学习是代数学方向,那么在这种情况下我主要的精力都放在了研究有限群理论上面,对于其他方向其实并没有太深入的了解。 在这种情况下,我只说一下我们代数方向本科毕业应该做到什么样的水平。
简单来说,乌拉尔联邦大学数学和计算机科学系《理论数学》专业本科毕业,学生可以选择《计算机数学》、《金融数学》、《数学物理》、《代数学》、《分析和泛函》、《几何学》、《概率论和随机方程》这几个大方向。 《代数学》方向需要在本科阶段学完整个有限群理论、主要的代数理论以便学生毕业后读研可以直接开始相关领域的科研,其中包括如下部分:
群理论方面
需要学完整个有限群理论的大部分截止1990年的结论,包括Burnsided定理、Schur-Zassenhaus定理、Frattini子群定理、Frobenius定理这几个主要的有限群领域的定理。
除此外需要详细学习一个有限群理论的前言课题,即群的谱方法(методы спектра)来利用Brobenius定理对有限群进行分类。
除此外还需要学习单群的分类问题,包括了解21个散在单群,虽然对于魔群(Monster group)只讲了这个群的“魔群月光理论”以及简单了解了一下魔群的构造,但是对于本科生已经很超纲了。
代数方面
需要学习完李代数初步课程,李代数需要学习到可解李代数、幂零李代数、半单李代数、卡丹分解这一部分,后面的话就不学了,算是给研究生数学系学习李群和李代数开个头。
微分几何是必须学习的,但是要求没那么深入,因为在俄罗斯一般高等级微分几何算作研究生课程,而本科至少需要了解到黎曼张量、超曲面、李导数这里。 因为学习李代数需要用到微分几何中的很多概念去推出李群。
三、数学系本科毕业论文和国考难度
国考(государственный экзамен)
总而言之,俄罗斯大学数学系的国考(гос.экзамен)基本上没什么压力,国考虽然需要把大一到大四所有课程从头到尾捋一遍,并且考题也是从大一到大四所有的专业课中抽,比如《数学分析》、《概率论》、《复变函数》、《高等代数》、《解析几何》、《数学物理方程》,但是国考最难的题目也就是工科数学的难度。
我们数学系学生一般把题目分为三个难度:
- 高中题目难度(школьная задача)
- 工科数学难度(задача инженерной математики)
- 数学系难度(сложная задача)
而大多数国考题目考虑到学生可能到大四时很多大一的东西也忘记了,所以题目会很简单,而且老师也会提供帮助,比如错了老师会指出来。 当然国考很有意思的一点就是大家考试时需要抽条,然后在纸上写下答案,然后上台在黑板上详细讲每一题的思路,底下老师会帮忙提问,和大一、大二、大三的正式考试不一样,国考一般老师不会问太难的补充问题,所以相当简单。
毕业论文(дипломная работа)
说实话,乌拉尔联邦大学数学系其他人毕业时是什么水平我也不太了解,但是我自己是《代数》方向的,我的毕业论文课题是“2nρ阶有限群的构造,ρ为一个奇素数”,这个课题涉及到一个数学领域的课题叫做“凯里问题”:
凯里分类问题”是一个这样的问题,即给定一个自然数n,给定其完整的拥有该阶数的有限群的完整分类。 这个问题有两个途径进行解决:第一个途径是固定群的阶数并求解拥有该阶数的所有非交换群的构造,利用的方法有求解其中心(即该群中所有可交换元素组成的集合 - 补充)、西洛子群的幂零性或者其他的方法(例如群的谱刻画方法等 - 补充),当然交换群的情形已经有了充分的研究。 对于这个问题可以参考很多数学的补充包和数据库,例如GAP 4.5.4,这里面给出了阶数小于2000的所有群的完整构造,除了1024阶群(近期1024阶群也已经构造完毕,有接近500亿个同构类 - 补充),一共包含4亿多个不同构造。 第二个途径是研究一个整的、拥有某种数学关系的阶的群,例如我们知道如果自然数n是一个质数,则拥有n阶的群只有一种。 另外一种古典方法求解的群为pq阶群,这里p、q皆为质数,若n=pq,则通过西洛定理可以求解出这种群的构造数目。 随着群的阶数的增加,对于某些问题的求解还存在很多未解决的点,例如我们取 n=aρ , a∉素数集合,(a,n)=1这种类型就很难求得其构造。
关于凯里分类问题的解释
总而言之,导师Gein A.S给我的任务就是,对这一课题的整体进行研究,得到某些一般性的结论,然后作为特例,利用我们研究出来的一般性的理论对2p,4p,8p阶群进行分类,如果到研究生阶段可以继续研究16p,32p阶群,博士阶段可以做到128p阶群,直至得到更加一般的结论。 那么接下来我们看一个我自己写的4p阶群的例子,注意这里4ρ阶群只是我论文中很小的一部分,整个论文有17页,这里只占4页内容。
有限群的阶为4ρ(ρ为一个奇素数)的构造的证明过程:




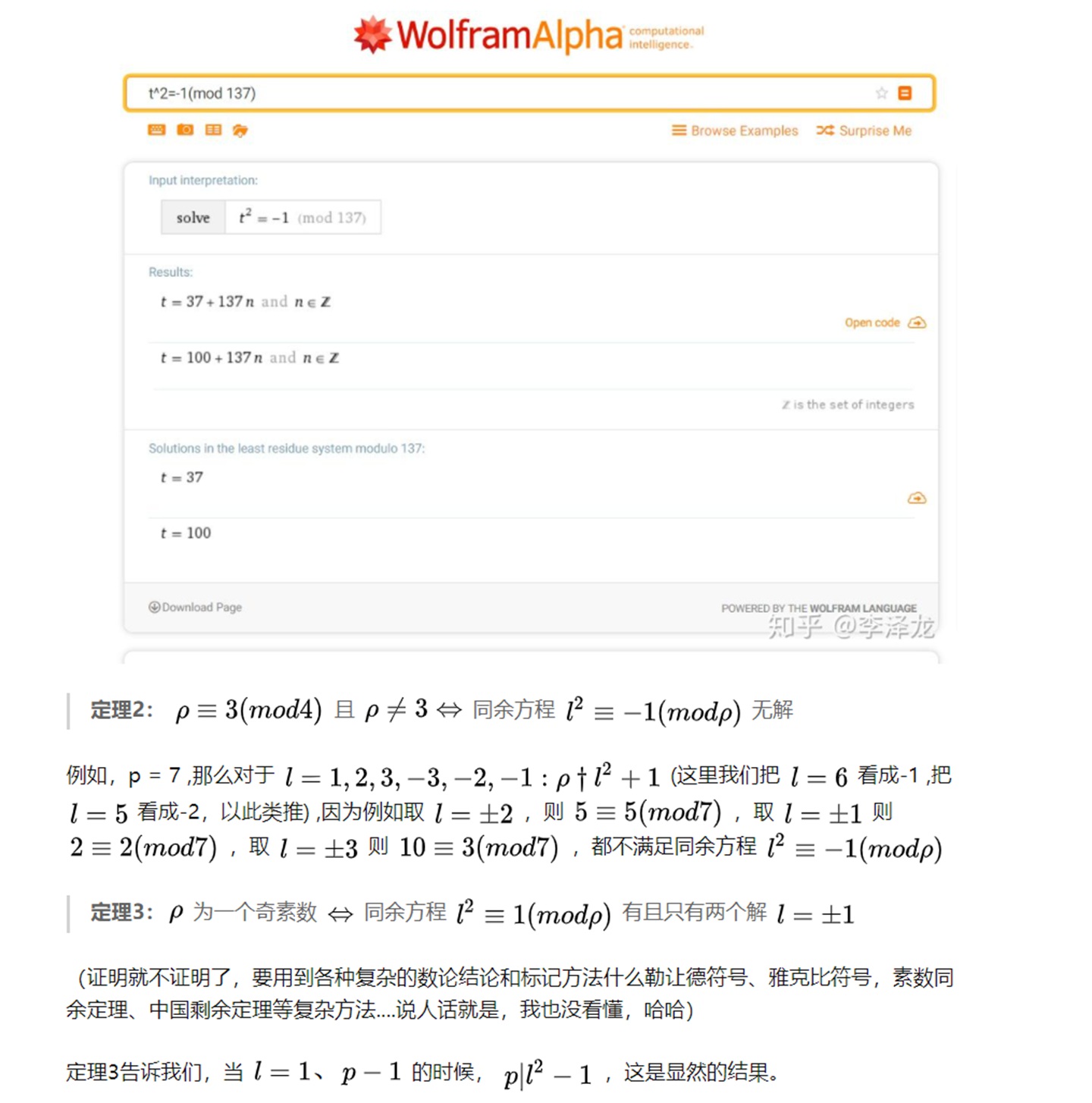





大致就是这样了, 如果这篇文章对各位有帮助,不妨收藏起来哦!
